2025青海高考数学试题(网传版 全国二卷+新高考II卷)
(网络收集)2025年全国二卷数学高考真题文字版
2,8,14,16,20平均数为
A.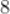
B.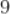
C.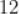
D.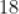
2. 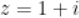 ,
,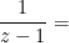
A.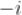
B.
C.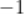
D.
3. 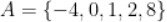 ,
,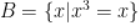 ,
,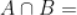
A.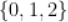
B.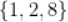
C.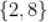
D.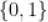
4. 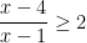 解集是
解集是
A.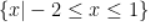
B.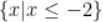
C. 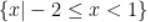
D.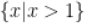
5. 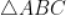 ,
,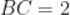 ,
,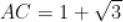 ,
,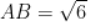 ,
,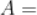
A.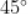
B.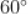
C.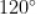
D.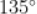
6. 抛物线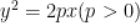 焦点
焦点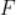 ,
,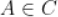 ,过
,过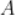 作
作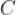 准线的垂线,垂足为
准线的垂线,垂足为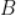 。若
。若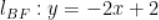 ,则
,则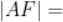
A.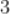
B.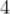
C.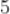
D.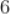
7. 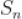 为等差数列
为等差数列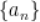 前
前 项和,
项和,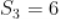 ,
,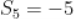 ,
,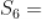
A.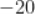
B.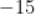
C.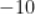
D.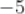
8. 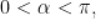 ,
,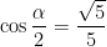 ,
,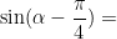
A.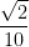
B.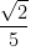
C.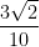
D.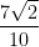
9. 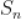 为等比数列
为等比数列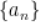 前
前 项和,
项和,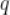 为
为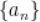 公比
公比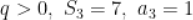 ,则
,则
A.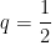
B.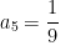
C.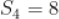
D.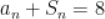
10. 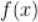 定义在
定义在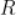 上奇函数,x>0时,
上奇函数,x>0时,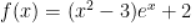 ,则
,则
A.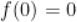
B. 当x<0时,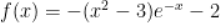
C.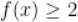 当且仅当
当且仅当
D. 是
是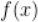 极大值点
极大值点
11. 双曲线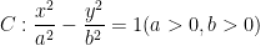 左、右焦点为
左、右焦点为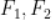 ,左、右顶点为
,左、右顶点为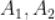 。以
。以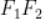 为直径的圆与
为直径的圆与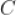 的一条渐近线交于
的一条渐近线交于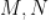 ,且
,且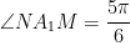 ,则
,则
A.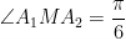
B.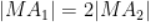
C.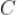 离心率为
离心率为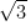
D. 当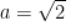 时,四边形
时,四边形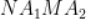 面积为
面积为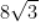
12.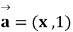 ,
,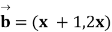 ,
,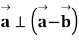 ,则
,则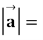 ____
____
13.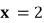 是
是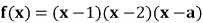 极值点,则
极值点,则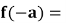 ____
____
14.一个底面半径为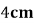 ,高为
,高为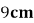 的封闭圆柱形容器,内有两个半径相等的铁球,则铁球半径的最大值为____
的封闭圆柱形容器,内有两个半径相等的铁球,则铁球半径的最大值为____ 。
。
15.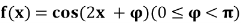 ,
,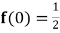
(1) 求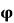 。
。
(2)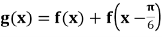 ,求
,求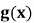 值域和单调区间。
值域和单调区间。
16.椭圆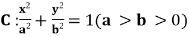 的离心率为
的离心率为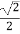 ,长轴长为
,长轴长为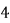 。
。
(1) 求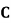 的方程。
的方程。
(2) 过点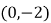 的直线
的直线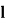 与
与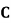 交于
交于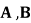 ,
,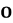 为坐标原点,若
为坐标原点,若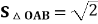 ,求
,求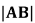 。
。
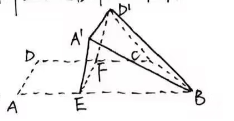
17.如图,四边形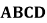 中,
中,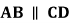 ,
,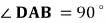 ,
,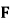 为
为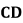 中点,
中点,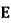 在
在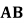 上,
上,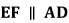 ,
,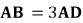 ,
,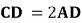 。将四边形
。将四边形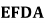 沿
沿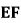 翻折至四边形
翻折至四边形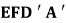 ,使得面
,使得面 与面
与面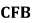 所成的二面角为
所成的二面角为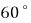 。
。
(1) 证明: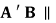 平面
平面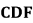 。
。
(2) 求面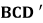 与面
与面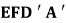 所成二面角的正弦值。
所成二面角的正弦值。
18.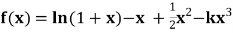 ,
,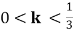 。
。
(1) 证明: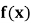 在
在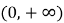 存在唯一极值点和唯一零点。
存在唯一极值点和唯一零点。
(2) 设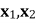 为
为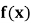 在
在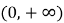 的极值点和零点。
的极值点和零点。
(i)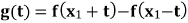 ,证明:
,证明: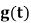 在
在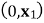 单减
单减
(ii) 比较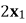 与
与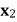 的大小,并证明。
的大小,并证明。
19.甲、乙乒乓球练习,每个球胜者得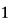 分,负者得
分,负者得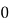 分,设每个球甲胜概率为
分,设每个球甲胜概率为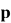 (
(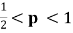 ),乙胜概率为
),乙胜概率为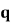 ,
,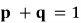 ,且各球胜负独立。对正整数
,且各球胜负独立。对正整数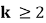 ,记
,记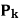 为打完
为打完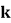 个球后甲比乙至少多得
个球后甲比乙至少多得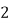 分的概率,
分的概率,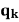 为打完
为打完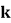 个球后乙比甲至少多得
个球后乙比甲至少多得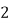 分的概率。
分的概率。
(1) 求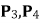 (用
(用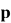 表示)。
表示)。
(2) 若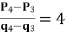 ,求
,求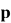 。
。
(3) 证明:对任意正整数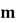 ,
,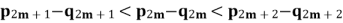 。(2)求面
。(2)求面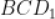 与面
与面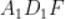 所成二面角的正弦值.
所成二面角的正弦值.




